AM-GM不等式(相加平均と相乗平均に関する不等式)の一般系は次の形で表されます。
\(n個の実数、a_1,a_2,\cdots,a_n>0\)について、
\(\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} \ge \sqrt[n]{a_1 a_2 \cdots a_n}\)
が常に成立する。
等号が成立するのは、
\(a_1=a_2=\cdots=a_n\)の時に限る。
不等式の左辺は相加平均(算術平均)、右辺は相乗平均(幾何平均)と呼ばれます。
なお、\(n\)個の実数\(\{a_k\}\)には\(0\)を許す(含める)場合もあります。
AM-GM不等式の変数置換
\(a_k>0\)ですから、その\(n\)乗根が一つ存在します。
それを\(x_k\)としますと、
\(x_k=\sqrt[n]{a_k}\)より
\(x_k^n=a_k\)となります。この変数でAM-GM不等式を表すと、
\( \displaystyle \frac{x_1^n+x_2^n+\cdots+x_n^n}{n} \ge x_1 x_2 \cdots x_n \)
となりますから、
AM-GM不等式を証明するには、
\( \displaystyle x_1^n +x_2^n+\cdots+x_n^n \ge n x_1 x_2 \cdots x_n \)
を証明すればよいわけです。
この不等式は、AM-GM不等式と同等です。
あらためてAM-GM不等式と同等な不等式を書き表すと、
\(n\)個の実数\(x_1,x_2,\cdots,x_n >0\)に対して、
\( \displaystyle x_1^n +x_2^n+\cdots+x_n^n ≧ n x_1 x_2 \cdots x_n \)
が成立する。
この不等式は、根号記号がないぶん、取り扱いやすく、初等的に証明しやすくなっています。
ちなみに、この不等式はムーアヘッドの不等式と呼ばれる不等式の特別な場合に該当しています。
ムーアヘッドの不等式はあまり知られていないようですが、多変数多項式の不等式ではその本質を表している不等式です。

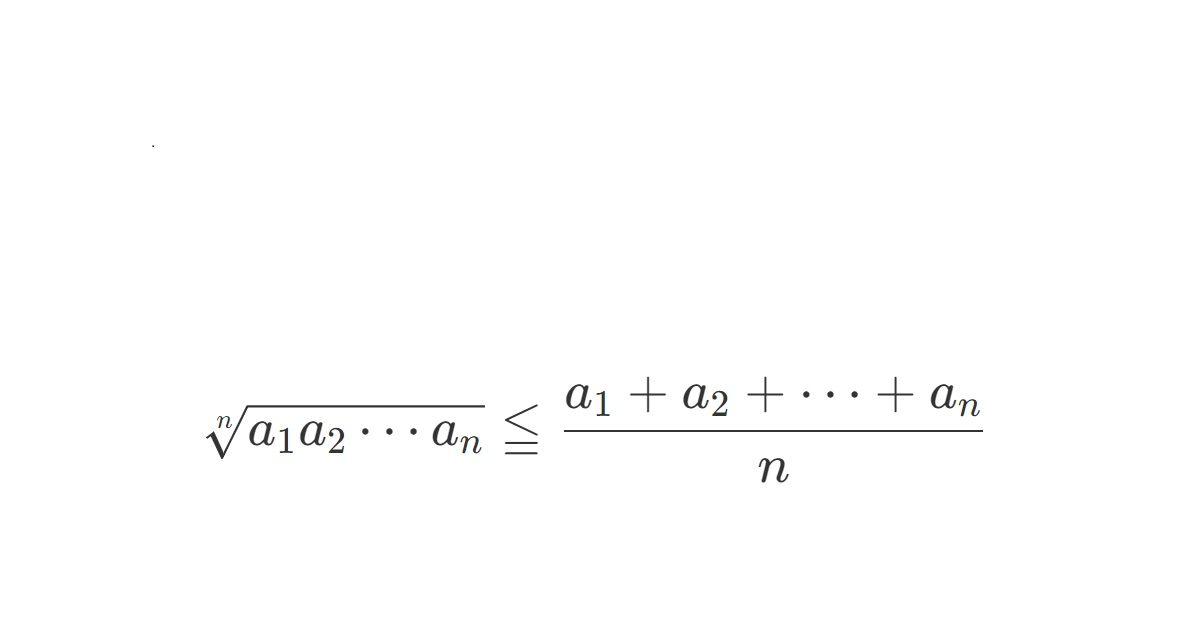
コメント