最も美しい不等式といえば、AM-GM不等式でしょう。
\(a,b>0\)とすると
\[\sqrt{ab}≦\frac{a+b}{2}\]
\(a_1,a_2,\cdots,a_n>0\)とすると
\[\sqrt[n]{a_1 a_2 \cdots a_n}≦\frac{a_1+a_2+\cdots+a_n}{n}\]
これがAM-GM不等式です。
AM-GM不等式の証明の概略
いろりろな証明方法が考えだされていますが、次の順序で証明するのが簡潔でわかりやすいと思います。変数はすべて正とします。
- \(n=2\)の場合を証明する
- 上記の不等式を繰り返して\(n\)が2のべきの場合を証明する。
- \(n\)が2のべきの場合をつかって一般の自然数の場合を証明する。
AM-GM不等式でn=2の場合
\(\displaystyle\sqrt{ab}≦\frac{a+b}{2}\)
この不等式の証明は、それほど難しくないと思います。
AM-GM不等式でn=2のべき場合
\(n=4,8,16,\cdots,2^k,\cdots\)の場合を証明します。
数学的帰納法で証明します。半分に区切って\(n=2\)の場合を繰り返し適用します。
半分の区切り方や繰り返し使う方法もいくつか考えられます。
AM-GM不等式でn=2のべき場合
\(n\)が2のべきでない場合を証明します。
これについては、項を増やしていったん項数を2のべきの状態にしたAM-GM不等式を利用します。
例えば、\(n=3\)の場合、
\(\displaystyle a_4=\frac{a_1+a_2+a_3}{3}\)とおいて、
\(n=4\)の場合に帰着させます。
すると、
\(\displaystyle \sqrt[4]{a_1 a_2 a_3 a_4}≦\frac{a_1+a_2+a_3+a_4}{4}\)の不等式を使うことができます。
\(a_4\)の式を代入して整理すると、\(n=3\)の場合のAM-GM不等式になります。
\(\displaystyle a_4=\sqrt[3]{a_1 a_2 a_3}\)とおいても同様に証明できます。
つまり、歯抜けになってる部分を相加平均もしくは相乗平均で埋め合わせて2のべきの形に帰着させることで証明することができます。

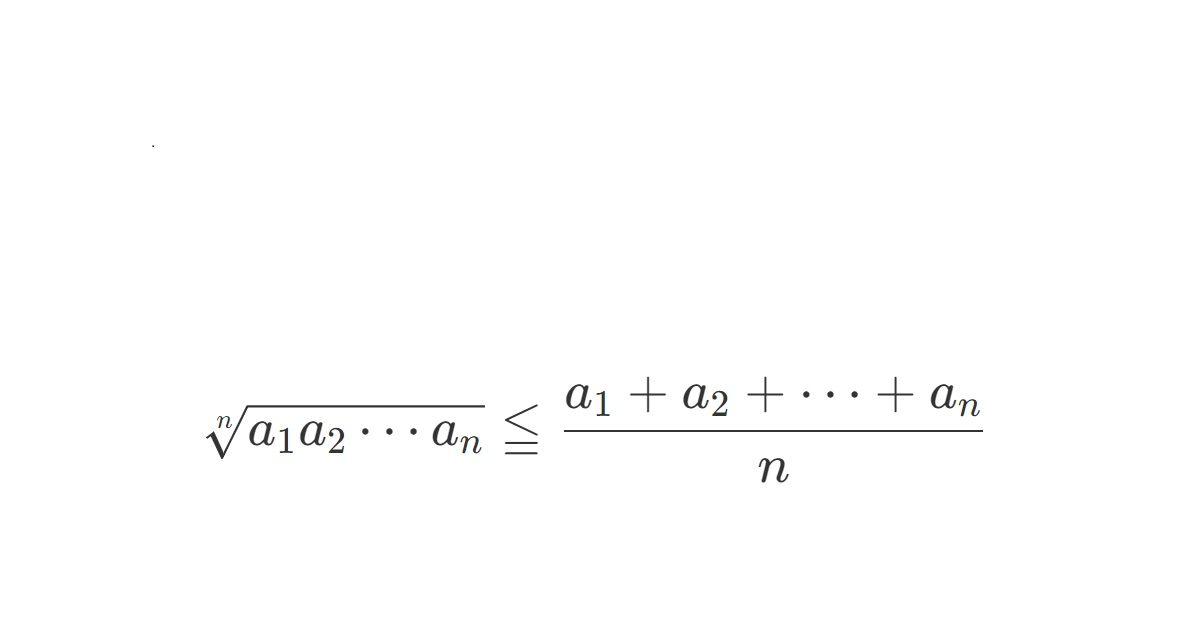

コメント