 行列解析
行列解析 [行列解析9.0]主要な記号一覧🔎
行列解析で使用している記号や用語の簡単な説明です。
 行列解析
行列解析  2.ユニタリ相似とユニタリ同値
2.ユニタリ相似とユニタリ同値  1.固有値・固有ベクトル・相似
1.固有値・固有ベクトル・相似  1.固有値・固有ベクトル・相似
1.固有値・固有ベクトル・相似  1.固有値・固有ベクトル・相似
1.固有値・固有ベクトル・相似  1.固有値・固有ベクトル・相似
1.固有値・固有ベクトル・相似  行列解析
行列解析 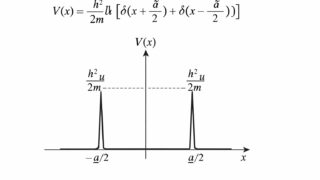 量子力学
量子力学  不等式
不等式