6.4.11.ブラウアの定理と削除行和に基づく固有値包含集合の一般化
次の系は、オストロフスキーとブラウアの定理に基づき、行列が非特異(可逆)であるための十分条件を与えるものである。
系 6.4.11.
\( A = [a_{ij}] \in M_n \) (\( n \ge 2 \))とする。次のいずれかの条件が成り立てば、行列 \(A\) は非特異である。
(a) (オストロフスキー) ある \(\alpha \in [0,1]\) が存在して、すべての \(i = 1, \ldots, n\) に対して次が成り立つ:
|a_{ii}| > R_i^{\alpha} C_i^{1-\alpha}
(b) (ブラウア) すべての異なる \(i, j = 1, \ldots, n\) に対して次が成り立つ:
|a_{ii}||a_{jj}| > R_i R_j
(演習)式 (6.4.1) と (6.4.7) を用いて、この系 (6.4.11) を証明せよ。
ブラウアの固有値包含集合 (6.4.8) は、ゲルシュゴリンのもの (6.1.2) よりも小さい。そのため、(6.2.8) に述べられた境界特性を満たさないことは驚くべきことではない。
(演習)次の行列を考える:
\begin{bmatrix}
1 & 1 & 1 \\
2 & 4 & 0 \\
1 & 0 & 2
\end{bmatrix}
この行列は既約であり、その固有値 \(\lambda = 0\) はブラウア集合 (6.4.8) の境界上にあることを確認せよ。 また、カッシーニの楕円 \(|z - 1||z - 2| = 2\) および \(|z - 1||z - 4| = 4\) は \(\lambda\) を通過するが、\(|z - 4||z - 2| = 2\) は通過しないことを説明せよ。
ブラウアの定理では、2つの削除行和の積を考えるが、これを拡張して \(A \in M_n\) の \(m\) 行について削除行和を取ることで、追加の固有値包含集合を構成することができる。
\bigcup_{i_1, \ldots, i_m \in I_m} \left\{ z \in \mathbb{C} : \prod_{k=1}^m |z - a_{i_k i_k}| \le \prod_{k=1}^m R^{\prime}_{i_k} \right\}
ここで \(I_m = \{ i_1, \ldots, i_m \in \{1, \ldots, n\} : i_1, \ldots, i_m \text{ は異なる}\}\) である。各 \(m\) に対して、このような集合は \(\binom{n}{m}\) 個存在する。 \(m=1\) の場合は \(n\) 個のゲルシュゴリン円板、\(m=2\) の場合はブラウアの \(n(n-1)/2\) 個のカッシーニの楕円が得られる。
しかし \(m \ge 3\) の場合、(6.4.12) の集合は一般に固有値包含集合とはならない。たとえば次の例で示される:
A = J_2 \oplus I_2, \quad
J_2 =
\begin{bmatrix}
1 & 1 \\
1 & 1
\end{bmatrix}
この行列では \(m = 3\) または \(4\) のとき、(6.4.12) の集合はすべて点 \(z = 1\) に縮退する。
(演習)行列 (6.4.13) の固有値が \(\lambda = 0, 1, 1, 2\) であることを示せ。 また、\(m=1\)、\(m=2\)、および \(m=3,4\) の場合の (6.4.12) の集合をスケッチせよ。 さらに、次の行列
A = J_2 \oplus I_n \in M_{n+2}
を考えることで、すべての \(m \ge 3\) について同様の現象が生じることを確認せよ。
(6.4.12) の問題点の一つは、削除行和がゼロを含む積を許してしまうことである。 ただし、行列 \(A\) が既約ならばこの問題は生じない(すべての \(R_i > 0\))。 しかし、たとえ \(A\) が既約であっても、(6.4.12) が固有値包含集合にならない場合がある。
その例として、次のような (6.4.13) の摂動行列を考える:
A_{\varepsilon} =
\begin{bmatrix}
1 & 1 & \varepsilon & \varepsilon \\
1 & 1 & 0 & 0 \\
\varepsilon & 0 & 1 & 0 \\
\varepsilon & 0 & 0 & 1
\end{bmatrix},
\quad 1 > \varepsilon \ge 0
このとき、\(A_{\varepsilon}\) の有向グラフは
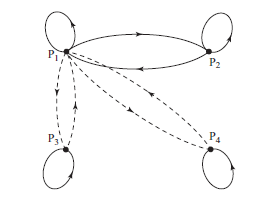
\(\varepsilon = 0\) で点線の弧が消える。
演習
\(\varepsilon \ne 0\) の場合、このグラフは強連結であり、行列 \(A_{\varepsilon}\) は既約である。 また、削除行和は \(R_1 = 1 + 2\varepsilon\)、\(R_2 = 1\)、\(R_3 = \varepsilon\)、\(R_4 = \varepsilon\) であり、 固有値は次の通りである:
\lambda_{\varepsilon} = 1, \, 1, \, 1 + \sqrt{1 + 2\varepsilon^2}, \, 1 - \sqrt{1 + 2\varepsilon^2}
この行列では、3つ以上の削除行和の積には少なくとも1つの因子として \(\varepsilon\) が含まれるため、\(\varepsilon\) が小さい場合、\(m=3\) および \(m=4\) に対して (6.4.12) の集合は固有値包含集合にならない。
では、なぜ (6.4.13) と (6.4.15) の行列では \(m=1\) と \(m=2\) の場合だけが適切なのか? それは、それらの有向グラフが長さ1および2のサイクルを持つが、3や4のサイクルを持たないためである。
この観察に基づき、次の既約な \(3 \times 3\) 行列を考える:
B =
\begin{bmatrix}
-2 & 1 & 6 \\
-18 & 0 & 1 \\
24 & 0 & 1
\end{bmatrix}
この行列は \(\lambda = 0\) を三重固有値として持つ。削除行和は \(R_1 = 7/24\)、\(R_2 = 1/4\)、\(R_3 = 24\) であり、ブラウア集合 (6.4.12) は次のように表される:
\{ z \in \mathbb{C} : |z + 2| |z - 1|^2 \le \tfrac{7}{4} \}
この集合は \(\lambda = 0\) を含まない。有向グラフ \(\Gamma(B)\) は長さ1、2、3のサイクルを含む。 ブラウアの定理により、\(m=2\) の3つの集合の和集合が \(\lambda\) を含むことが保証される。 そのうち1つの集合、
\{ z \in \mathbb{C} : |z + 2||z - 1| \le 7 \}
は行列 \(B\) の全ての固有値を含む。この集合は、有向グラフ \(\Gamma(B)\) の唯一の長さ2のサイクルに対応している。
一般に、有向グラフ \(\Gamma\) が強連結であるとは、任意のノードから他の任意のノードへの有向パスが存在することをいう。 また、\(\Gamma\) が弱連結であるとは、各ノードが少なくとも1つの非自明なサイクル(自己ループでない閉路)に含まれることを意味する。
行列 \(A \in M_n\) の有向グラフ \(\Gamma(A)\) が強連結であることと、\(A\) が既約であることは同値である。 また、\(\Gamma(A)\) が弱連結であるとき、\(A\) を弱既約という。 すなわち、各 \(i = 1, \ldots, n\) に対して、行 \(i\) に少なくとも1つの非対角要素 \(a_{ij}\) が存在し、そこから非零要素の連鎖 \(a_{k_1 k_2}, a_{k_2 k_3}, \ldots, a_{k_{m-1} k_m}\) が存在して \(k_1 = j_i, k_m = i\) となる場合である。 この条件は (6.2.7) における性質SCの半分に相当し、計算上は (6.2.23) と同様の形で表すと便利である。
行列解析の総本山
総本山の目次📚

記号の意味🔎




コメント