ダブルデルタ関数ポテンシャルの波動関数

数学徒が量子力学の数理にアプローチするための第一歩として、物理の教科書に登場する演習題を「数学の問題」という視点から解いてみました。量子力学の問題は、数学的に見ても非常に深みのある構造を持っています。

本記事では、「ダブルデルタ関数ポテンシャル」を具体例に挙げ、正のエネルギーにおける「散乱状態と確率流の関係」、および負のエネルギーにおける「偶対称・奇対称な束縛状態の存在条件」を詳しく解説します。物理的な背景を踏まえつつ、数学的な定義や解の振る舞いの意味を、数学を志す方に向けて丁寧に紐解いていきます。

問題

１次元の(定常状態)シュレディンガー方程式について、

\;\\
-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} \psi(x)+V(x) \psi(x)  =E \psi(x) \\
\;

ポテンシャルが

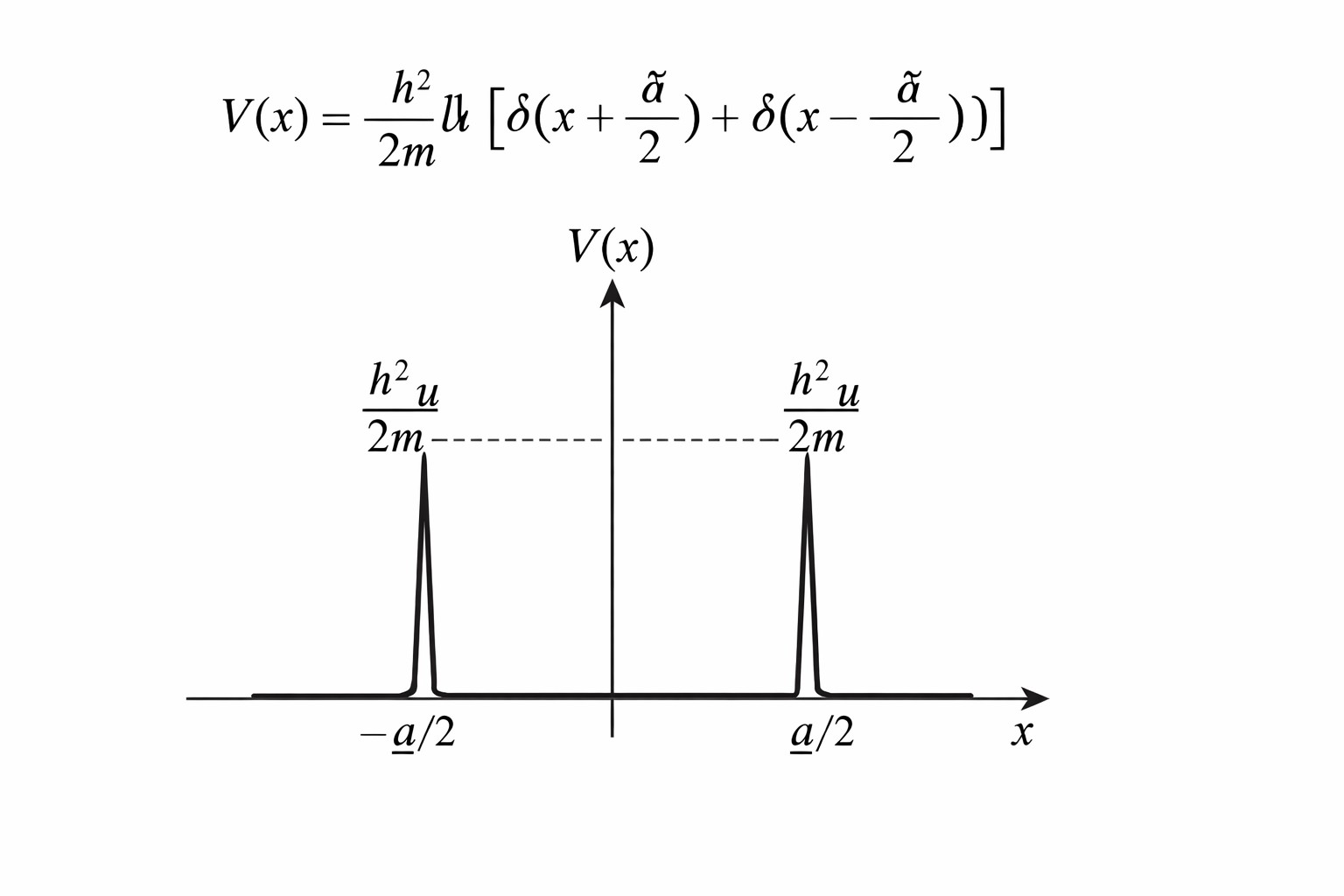
V(x)=\frac{\hbar^2}{2m}u \left[\delta(x+\frac{a}{2})+\delta(x-\frac{a}{2}) \right] \;\\
\qquad \\　a>0,\;u\neq 0, \; δ(x):\text{デルタ関数}

で与えられる 1 次元量子系について考える。

ここで、\(x\)の領域を下記の３つに分割する。

\begin{cases}
\text{I}: x<-a/2,\quad \\
\text{II}: -a/2<x<a/2,\quad \\
\text{III}: x>a/2
\end{cases}

\( \hbar=\frac{h}{2\pi} \)（換算プランク定数）、\(h\)（プランク定数）、\(\pi\)（円周率）、\(m\)（質量）や\(E\)（エネルギー）は実数の定数です。

定常状態とは、時間依存がない状態という意味です。方程式に時間を表す変数\(t\)がないので、そのぶん解きやすくなります。

(1)正のエネルギー固有値Eををもつ状態

k=\sqrt{ \frac{2mE}{ \hbar ^2}}

として各領域での確率の流れの密度を求め、それらの間の関係を議論せよ。
ただし,\(x\)の正方向からの入射波は存在しないものとし、\(x\)の負方向からの入射波の係数が1になるように規格化せよ。

(2)負のエネルギー固有値Eをもつ状態

波動関数が対称性

φ_+(x) = φ(-x) \\
または、\\
φ_-(x) = -φ(-x)

をもつ束縛状態が存在するための条件を求めよ。

問題の解説

(1)正のエネルギー固有値Eををもつ場合

なにはともあれ、波動関数を求めなければこの問題は解けない。

\;\\
-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} \psi(x)+V(x) \psi(x)  =E \psi(x) \\
\;

\;\\
\left[ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} +V(x) \right]  \psi(x) =E \psi(x) \\
\;

なにはともあれ、まず波動関数を求める(つまりシュレディンガー方程式の解を求める)ことが本問題を解くために必要である。

ポテンシャル

さて、シュレディンガー方程式の中にある関数\(V(x)\)はポテンシャルと呼ばれる\(x\)の関数である。問題文で\(V(x)\)の関数がなんであるのか明示されているが、物理では\(V(x)\)がデルタ関数という数学で扱いにくい関数が平然と使われる。

デルタ関数

デルタ関数は、\(x=0\)で無限大、\(x \ne=0\)で0となる超関数の事であるが、イメージだけで議論できるし、イメージでできるようにならないと取り組めないので、厳密な定義は割愛する。

しかしデルタ関数の定義を単純なグラフのイメージでしかとらえていない場合、いざデルタ関数を使った計算をどうするのか、ある程度の慣れがないと行き詰ってしまう。物理では、特に極限操作については、直感的な感覚に従って進めることが多いので、数学屋にとっては面食らう場面が多いのだ。物理では厳密な証明は後回しにし、使える公式は証明など気にしないで使っていく事が物理数学を使いこなすコツである。

各領域の波動関数

シュレディンガー方程式の解が波動関数なのだが、この問題のように、ポテンシャル関数\(V(x)\)によっては、\(x\)の範囲をいくつかの領域に区切り、領域毎に解を求めて、それらをつなぎ合わせて波動関数を構成するという手法をとる。

\psi(x)=\begin{cases}
\text{I}: \psi_{I}(x) \quad  & \text{if } \;  x \lt -a/2 \quad \\
\text{II}:\psi_{II}(x) \quad  & \text{if } \;  -a/2  \lt x \lt a/2 \quad \\
\text{III}: \psi_{III}(x) \quad  & \text{if } \; a/2 \lt x
\end{cases}

そこで、それぞれの領域I、II、IIIにおいて部分的な波動関数をもとめ、それら求めた波動関数を領域の境界で接続して波動関数を求めていく。

各領域は、通常(特異な点を含まない)の微分方程式なので、初等的な微積分の解法で解くことができる。つまり、各領域においての波動関数は、デルタ関数を含まない微分方程式

-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}    \psi(x) =E \psi(x)

を解けばよい。この解は、\(E\)が正の場合と負の場合で解の形がわかれる。

\(E\)が正の場合の一般解は、

Ae^{ikx}+Be^{-ikx}\\
A,Bは積分定数、k=\sqrt{\frac{2mE}{\hbar^2}}

である。

入射波と反射波

この一般解の\(Ae^{ikx}\)の部分を入射波、\(Be^{-ikx}\)の部分を反射波と呼ぶ。

入射波は物理的には、右(x軸方向)に進む波であり、反射波は左に進む波だと捉える。

接続条件

関数\(\psi_{II}(x),\psi_{III}(x)\)が\(x=a/2\)で接続しているという条件を式で表すと、通常は

\psi_{III}(a/2)=\psi_{II}(a/2) \\
\psi_{III}'(a/2)=\psi_{II}'(a/2)

としたいところであるが、デルタ関数が含まれた微分方程式では、特異な点での接続条件が下記のように変わる。

\psi_{III}(a/2):=\lim_{\epsilon \rightarrow0 }\psi_{III}(a/2+\epsilon)

忌まわしいデルタ関数の特異な点での接続条件は下記のようになる。

\psi_{III}(a/2)=\psi(a/2) =\psi_{II}(a/2) \\
-\frac{\hbar^2 }{2m} \left( \psi_{III}'(a/2)-\psi_{II}'(a/2)  \right) + \frac{\hbar^2 u}{2m} \psi(a/2)=0

\int_{a/2-\epsilon}^{a/2+\epsilon} \left[ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} \psi(x)+V(x) \psi(x) dx   \right] 
= \int_{a/2-\epsilon}^{a/2+\epsilon}E \psi(x) dx \\
-\frac{\hbar^2}{2m} \int_{a/2-\epsilon}^{a/2+\epsilon}  \frac{d^2}{dx^2} \psi(x)  dx + \int_{a/2-\epsilon}^{a/2+\epsilon} V(x) \psi(x) dx    
= \int_{a/2-\epsilon}^{a/2+\epsilon}E \psi(x) dx \\
-\frac{\hbar^2}{2m} \left[ \psi_{III}'(a/2+\epsilon) - \psi_{II}'(a/2-\epsilon)\right] +\int_{a/2-\epsilon}^{a/2+\epsilon} V(x) \psi(x) dx \\   
= E \int_{a/2-\epsilon}^{a/2+\epsilon} \psi(x) dx 

\int_{a/2-\epsilon}^{a/2+\epsilon} V(x) \psi(x) dx \\
=\int_{a/2-\epsilon}^{a/2+\epsilon} \frac{\hbar^2}{2m}u \left[\delta(x+\frac{a}{2})+\delta(x-\frac{a}{2}) \right]  \psi(x) dx 
\\
= \frac{\hbar^2}{2m}u  \int_{a/2-\epsilon}^{a/2+\epsilon}\delta(x-\frac{a}{2})  \psi(x) dx 

\int_{-\infty}^{\infty}  δ(x) \psi(x) \;dx = \psi(x)

-\frac{\hbar^2 }{2m} \left( \psi_{III}'(a/2)-\psi_{II}'(a/2)  \right) + \frac{\hbar^2 }{2m} u\psi(a/2)=0

確率の流れの密度

確率の流れの密度は、\(j\)の記号を使って表す。規格化された（下記の条件を満たす）波動関数\(\psi(x)\)

にたいして、確率密度は、

j=\frac{\hbar}{2mi}\left( \psi(x)^* \frac{d\psi}{dx} - \psi(x) \frac{d\psi^*}{dx}  \right)
\\

で定義される。例えば、波動関数が、

の場合、確率の流れの密度は、

j=\frac{\hbar}{2mi}
[ (A^* e^{-ikx}+B^* e^{ikx})(ik A e^{ikx}-ik B e^{-ikx}) \\
 \quad  - (A e^{ikx}+B e^{-ikx}) (-ikA^* e^{-ikx}+ikB^* e^{ikx})   ]\\
=\frac{\hbar}{2mi} 
[ ik |A|^2 -ik A^*B e^{-2ikx} +ikB^*A e^{2ikx} -ik|B|^2 \\
 +ik|A|^2 -ik A B^* e^{2ikx} +ik B A^* e^{-2ikx} -ik |B|^2
] \\
=\frac{\hbar}{2mi} [2 ik |A|^2   -2ik|B|^2   ]\\
\; \\
=\frac{\hbar k}{m} \left( |A|^2   -|B|^2 \right)\\

ここまでで問題（１）の部分の問題の意味の説明を終わる。

(2)負のエネルギー固有値Eををもつ場合

次に問題（２）の部分の説明をする。

-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}    \psi(x) =E \psi(x)

\(E\)が負の場合、この微分方程式の一般解は、

Ae^{kx}+Be^{-kx}\\
A,Bは積分定数、k=\sqrt{-\frac{2mE}{\hbar^2}}

実は波動関数の値は有限でなければならないという制約がある。そのため、この一般解は波動関数の体をなさない。しかし、この解の一部をきりとってつなぎ合わせる事で波動関数を作ることができる。問題（２）は、どういう条件の時に波動関数を作ることができるのかという問である。

波動関数のパリティ

実は、ポテンシャルが左右対称(偶関数)である場合、波動関数は偶関数か奇関数でなければならない。偶関数の場合偶パリティ（正のパリティ）、奇関数の場合奇パリティ（負のパリティ）と呼ぶ。

解答例

(1) 正のエネルギー固有値（散乱状態）

波動関数を求める

３つの領域に分割して考える。

\text{I}: x<-a/2,\quad
\text{II}: -a/2<x<a/2,\quad
\text{III}: x>a/2

負方向（左）からのみ入射があり，その係数を 1 に規格化すると波動関数は、

\psi(x)=
\begin{cases}
e^{ikx}+R e^{-ikx}, & x<-a/2,\\
A e^{ikx}+B e^{-ikx}, & -a/2<x<a/2,\\
T e^{ikx}, & x>a/2
\end{cases}

と表すことができる。

確率流密度

j=\frac{\hbar}{m}\,\mathrm{Im}\!\left(\psi^*\frac{d\psi}{dx}\right)

平面波 \(Ce^{\pm ikx}\) に対して

j=\pm\frac{\hbar k}{m}|C|^2

となる。したがって各領域で確率密度を計算すると、

\begin{aligned}
j_{\mathrm{I}} &= \frac{\hbar k}{m}(1-|R|^2),\\
j_{\mathrm{II}} &= \frac{\hbar k}{m}(|A|^2-|B|^2),\\
j_{\mathrm{III}} &= \frac{\hbar k}{m}|T|^2
\end{aligned}

となる。

確率流の保存

j_{\mathrm{I}}=j_{\mathrm{II}}=j_{\mathrm{III}}

よって

|R|^2+|T|^2=1

(2) 負のエネルギー固有値（束縛状態）

E=-\frac{\hbar^2\kappa^2}{2m},\qquad \kappa>0

ポテンシャルは偶関数であるため，波動関数は偶対称または奇対称に分類できる。

デルタ関数の位置 \(x_0=\pm a/2\) における接続条件は

\psi'(x_0+0)-\psi'(x_0-0)=u\,\psi(x_0)

(a) 偶対称束縛状態

\phi_+(x)=\phi_+(-x)

中央領域では

\phi_+(x)=A\cosh(\kappa x)

となり，接続条件から

\kappa=\frac{u}{2}\left(1+e^{-\kappa a}\right)

を満たすとき，偶対称束縛状態が存在する。

(b) 奇対称束縛状態

\phi_-(x)=-\phi_-(-x)

中央領域では

\phi_-(x)=A\sinh(\kappa x)

接続条件より

\kappa=\frac{u}{2}\left(1-e^{-\kappa a}\right)

を満たすとき，奇対称束縛状態が存在する。

まとめ

散乱状態では確率流は保存され，\(|R|^2+|T|^2=1\) が成り立つ。 束縛状態は偶対称・奇対称の 2 種類に分類され， それぞれ対応する条件式を満たす場合に存在する。