6.1.6系
以下はゲルシュゴリン円盤定理の重み付き版に関する系の日本語訳である。対角行列での相似変換を導入することで、固有値の包含領域をより柔軟に(かつ必要に応じて任意の精度で)絞り込むことができる。
系 6.1.6. \(A=[a_{ij}]\in M_n\) を任意に取り、正の実数 \(p_1,p_2,\dots,p_n\) を与える。すると行列 \(A\) の固有値は次の \(n\) 個の円盤の和集合に含まれる。
\bigcup_{i=1}^n \left\{ z\in\mathbb{C} : |z-a_{ii}| \le \frac{1}{p_i}\sum_{j\ne i} p_j\,|a_{ij}| \right\} = G(D^{-1} A D)
ここで \(D=\mathrm{diag}(p_1,\dots,p_n)\) とし、右辺は \(D^{-1}AD\) に対するゲルシュゴリン集合を表す。さらに、これら \(n\) 個の円盤のうち \(k\) 個の和集合 \(G_k(D^{-1}AD)\) が残りの \(n-k\) 個の円盤と互いに交わらないならば、\(G_k(D^{-1}AD)\) の中には代数的重複度を考えてちょうど \(k\) 個の固有値が含まれる。
同様に転置行列との相似変換を考えると、列方向の重み付き円盤による包含も得られる。すなわち次の集合にも固有値は含まれる。
\bigcup_{j=1}^n \left\{ z\in\mathbb{C} : |z-a_{jj}| \le p_j \sum_{i\ne j} \frac{1}{p_i}\,|a_{ij}| \right\} = G(D A^{T} D^{-1})
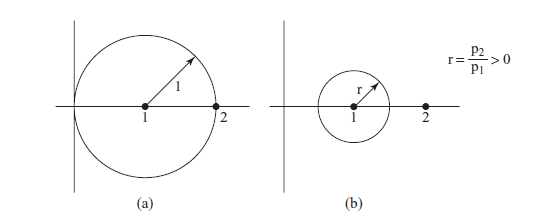
重み \(p_i\) を自由に選べることで、円盤の中心や半径を調節できるため、元の(無重み)ゲルシュゴリン円盤よりもはるかに良い(=狭い)包含領域を得られる場合がある。例えば行列
A=\begin{pmatrix}1 & 1\\ 0 & 2\end{pmatrix}
は固有値 \(1\) と \(2\) を持つが,無重みのゲルシュゴリン円盤をそのまま使うとかなり粗い推定しか得られない(図 6.1.7(a))。一方で適切な正の重み \(p_1,p_2\) を取れば円盤を狭められ,任意に良い精度で固有値を囲むことが可能である(図 6.1.7(b))。
(演習)次の行列を考える。
A=\begin{bmatrix}
7 & -16 & 8\\
-16 & 7 & -8\\
8 & -8 & -5
\end{bmatrix}
ゲルシュゴリンの定理を用いて,この行列 \(A\) の固有値の位置およびスペクトル半径についてわかる範囲で述べよ。次に任意の正の対角行列 \(D=\mathrm{diag}(p_1,p_2,p_3)\) を取り,\(D^{-1}AD\) に対する重み付きゲルシュゴリン円盤を用いて固有値位置の改善が得られるか調べよ。最後に実際の固有値を計算し,推定がどの程度当たっていたかを検討せよ。
(演習)なぜ行列 \(A\) のすべての固有値が,正の主対角成分を持つ任意の対角行列 \(D\) についての集合 \( \bigcap_{D} G(D^{-1}AD) \) に含まれるかを説明せよ(ここで交差は全てのそのような \(D\) に関する交差を示す)。
最後に補足すると,重み(自由パラメータ)を導入する考え方はスペクトル半径に関する不等式(式 (6.1.5))をより一般的な形に拡張する際にも有効である。適切な重みを選ぶことで得られる最小上界を最適化すれば,スペクトル半径に対するより厳密な上界が得られる。
行列解析の総本山
総本山の目次📚

記号の意味🔎




コメント