補題 2.1.10:ユニタリ行列のブロック構造
ユニタリ行列 \( U \in M_n \) を次のようにブロック分割します:
U = \begin{bmatrix}
U_{11} & U_{12} \\
U_{21} & U_{22}
\end{bmatrix}
ここで \( U_{11} \in M_k \) とします。このとき以下が成り立ちます:
- \( \operatorname{rank} U_{12} = \operatorname{rank} U_{21} \)
- \( \operatorname{rank} U_{22} = \operatorname{rank} U_{11} + n - 2k \)
特に、\( U_{12} = 0 \) となるのは \( U_{21} = 0 \) のときに限り、その場合 \( U_{11} \) および \( U_{22} \) はユニタリ行列である。
証明
階数に関する2つの主張は、補題 (0.7.5) の「相補的零空間の法則」と、ユニタリ行列の逆行列が共役転置になる性質
U^{-1} =
\begin{bmatrix}
U_{11}^* & U_{21}^* \\
U_{12}^* & U_{22}^*
\end{bmatrix}
を用いることで直ちに従います。
練習問題
上の補題を用いて、ユニタリ行列が上三角であることと、それが対角行列であることが同値であることを示しなさい。
平面回転行列とハウスホルダー行列
平面回転(Plane Rotation)やハウスホルダー行列(Householder Matrix)は、基本的かつ重要なユニタリ行列の例であり、基本的な行列分解において中心的役割を果たします。
例 2.1.11:平面回転
\( 1 \leq i < j \leq n \) とし、次のように定義された行列を考えます:
単位行列の \( i,i \) および \( j,j \) 成分を \( \cos\theta \) に置き換え、\( i,j \) 成分を \( -\sin\theta \)、\( j,i \) 成分を \( \sin\theta \) に置き換えたものを
U(\theta; i, j)
と呼び、これは「平面回転行列」または「ギブンズ回転(Givens Rotation)」と呼ばれます。
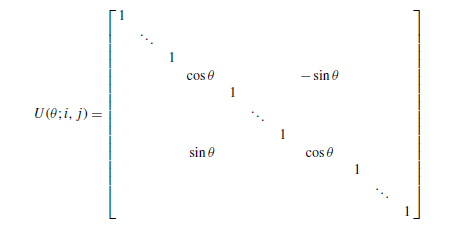
この行列 \( U(\theta; i, j) \in M_n(\mathbb{R}) \) は任意の \( \theta \in [0, 2\pi) \) に対して実直交行列であることを確認しなさい。
この行列は \( \mathbb{R}^n \) の \( i,j \) 平面内での角度 \( \theta \) の回転を行います。左から掛けると行列の第 \( i \) 行と \( j \) 行のみが影響を受け、右から掛けると第 \( i \) 列と \( j \) 列のみが変化します。
さらに、次を確認しなさい:
U(\theta; i, j)^{-1} = U(-\theta; i, j)
例 2.1.12:ハウスホルダー行列
ゼロでないベクトル \( w \in \mathbb{C}^n \) に対し、ハウスホルダー行列 \( U_w \in M_n \) は次で定義されます:
U_w = I - 2 (w^* w)^{-1} w w^*
\( w \) が単位ベクトルである場合、式は単純化されて次のようになります:
U_w = I - 2 w w^*
練習問題
- ハウスホルダー行列 \( U_w \) がユニタリかつエルミートであることを示しなさい。よって \( U_w^{-1} = U_w \) が成り立つ。
- \( w \in \mathbb{R}^n \) の場合、\( U_w \) は実直交かつ対称行列であることを示しなさい。また、その固有値がすべて \( \pm 1 \) である理由を述べなさい。
- \( x \perp w \) のとき \( U_w x = x \)、また \( U_w w = -w \) を示し、\( U_w \) が \( w^\perp \) 上で恒等写像、\( w \) の張る一次元部分空間上で反射であることを説明しなさい。
- 式 (0.8.5.11) を使って、任意の次元 \( n \) において \( \det U_w = -1 \) を示しなさい。従って \( U_w \in M_n(\mathbb{R}) \) は常に実直交行列だが、決して「正の回転行列」(行列式が +1 のもの)ではない。
- 式 (1.2.8) を用いて、ハウスホルダー行列の固有値が常に \( -1, 1, \dots, 1 \) であり、行列式が常に \( -1 \) であることを説明しなさい。
- \( n \geq 2 \)、\( x, y \in \mathbb{R}^n \) が単位ベクトルのとき、\( x = y \) ならば \( x \) に直交する任意の単位ベクトル \( w \) を選び、そうでなければ \( w = x - y \) とおきなさい。そのとき \( U_w x = y \) を示しなさい。従って、任意のベクトル \( x \in \mathbb{R}^n \) は、ユークリッドノルムが等しい \( y \in \mathbb{R}^n \) にハウスホルダー行列で変換可能である。
- ただし \( \mathbb{C}^n \) の場合は異なる。例えば、\( U_w e_1 = i e_1 \) となるような \( w \in \mathbb{C}^n \) が存在しないことを示しなさい。
ハウスホルダー行列とユニタリなスカラ行列を組み合わせることで、ユークリッドノルムが等しい任意の2つのベクトル間で変換可能なユニタリ行列を構成できます。


コメント